The expression for the capacitance of a parallel-plate capacitor that has plates of area \(A\) separated by a distance \(d\) is given in Example 26. 2.

(a) Show that the expression for a spherical capacitor, given in Example 26. 4, reduces to the expression for a parallel-plate capacitor in the limit that \(R_{1}\) approaches \(R_{2}\), with \(d=R_{2}-R_{1}\).

(b) Show that the expression for a cylindrical capacitor, given in Example 26. 3 , reduces to the expression for a parallel-plate capacitor in the limit that \(R_{1}\) approaches \(R_{2}\), with \(d=R_{2}-R_{1}\). (You might find the Taylor series expansion of \(\ln (1+x)\) useful.)

Data from Example 26. 2

What is the capacitance of a parallel-plate capacitor that has a plate area \(A\) and a plate separation distance \(d\) ?

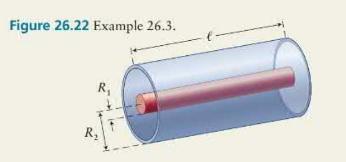
Data from Example 26.3

Figure \(\mathbf{2 6 . 2 2}\) shows a coaxial capacitor consisting of two concentric metal cylinders 1 and 2, of radii \(R_{1}\) and \(R_{2}>R_{1}\), and both of length \(\ell \gg R_{2}\). Both cylinders are made of metal. What is the capacitance of this arrangement?

Data from Figure 26.23

Data from Example 26.4

What is the capacitance of a spherical capacitor consisting of two concentric conducting spherical shells of radii \(R_{1}\) and \(R_{2}>R_{1}\) ?

Figure 26.22 Example 26.3. R, R