The half-life (t_1/2) of a radioactive species is the time it takes for half of the species to emit radiation and decay (turn into a different species). If a quantity N₀ of the species is present at time t = 0, the amount present at a later time t is given by the expression 

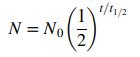
Each decay event involves the emission of radiation. A unit of the intensity of radioactivity is a curie (Ci), defined as 3.7x10¹⁰ decay events per second. 

A 300,000-gallon tank has been storing aqueous radioactive waste since 1945. The waste contains the radioactive isotope cesium-137 (¹³⁷Cs), which has a half-life of 30.1 years and a specific radioactivity of 86.58 Ci/g. The isotope undergoes beta decay to radioactive barium-137, which in turn emits gamma rays and decays to stable (nonradioactive) barium with a half-life of 2.5 minutes. The concentration of ¹³⁷Cs in 2013 was 2.50x10^-3 g/L. 

(a) What fraction of the ¹³⁷Cs would have to decay for the level of cesium-related radioactivity of the contents to be 1.00x10^-3 Ci/L? What total mass of cesium (kg) would that loss represent? In what year would that level be reached? 

(b) What was the concentration of ¹³⁷Cs in the tank (g/L) when the waste was first stored? 

(c) Explain why the radioactive cesium in the tank poses a significant environmental threat while the radioactive barium does not.

Transcribed Image Text:

t/1/2 N = No