You have been assigned the task of measuring the equilibrium constant for the reaction N₂O₄ ⇌2NO₂ as a function of temperature. To do so, you evacuate a rigid 2-liter vessel equipped with a pressure gauge, fill the vessel with a mixture of NO₂ and N₂O₄, and then heat it to T0 ˆ 473 K, a temperature at which you know the gas is essentially pure NO_2. The gauge pressure at this point is noted to be 1.00 atm. You then decrease the temperature in stages, recording the equilibrium gauge pressure at each temperature. The data are as follows:

(a) How many gram-moles of NO₂ are in the vessel at 473 K? 

(b) The reaction equilibrium constant is

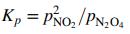
where p_NO2 and p_N2O4 are the equilibrium partial pressures of NO₂ and N₂O₄. Derive an equation or a series of equations for calculating Kp(atm) from specified values of T and Pgauge. (Suggestion: Begin by defining n1 and n2 as the moles of NO₂ and N₂O₄ present at equilibrium.) Then calculate Kp for T ˆ 350 K, 335 K, 315 K, and 300 K. (Suggestion: Use a spreadsheet.) 

(c) The equilibrium constant should vary with temperature according to the relation 

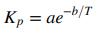
Use the results of Part (b) to determine the values of a and b by curve-fitting. 

Methanol is synthesized from carbon monoxide and hydrogen in the reaction 

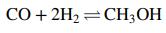
A process flowchart is shown below. 

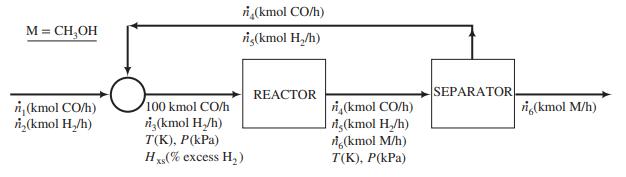
The fresh feed to the system, which contains only CO and H₂, is blended with a recycle stream containing the same species. The combined stream is heated and compressed to a temperature T(K) and a pressure P(kPa) and fed to the reactor. The percentage excess hydrogen in this stream is H_xs. The reactor effluent—also at T and P—goes to a separation unit where essentially all of the methanol produced in the reactor is condensed and removed as product. The unreacted CO and H₂ constitute the recycle stream blended with the fresh feed. 

Provided that the reaction temperature (and hence the rate of reaction) is high enough and the idealgas equation of state is a reasonable approximation at the reactor outlet conditions (a questionable assumption), the ratio 

approaches the equilibrium value, which is given by the expression 

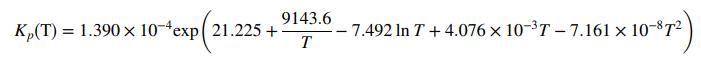
In these equations, pi is the partial pressure of speciesi in kilopascals (i = CH₃OH, CO, H₂) and T is in Kelvin. 

(a) Suppose P = 5000 kPa, T = 500 K, and the percentage excess of hydrogen in the feed to the reactor (H_xs) = 5.0%. Calculate ṅ₄; ṅ₅, and ṅ₆, the component flow rates (kmol/h) in the reactor effluent. [Suggestion: Use the known value of H_xs , atomic balances around the reactor, and the equilibrium relationship, K_pc = Kp(T), to write four equations in the four variables ṅ₃ to ṅ₆; use algebra to eliminate all but ṅ₆; and use Goal Seek or Solver in Excel to solve the remaining nonlinear equation for ṅ6.] Then calculate component fresh feed rates (ṅ₁ and ṅ₂) and the flow rate (SCMH) of the recycle stream.

(b) Prepare a spreadsheet to perform the calculations of Part (a) for the same basis of calculation (100 kmol CO/h fed to the reactor) and different specified values of P(kPa), T(K), and H_xs(%). The spreadsheet should have the following columns: 

A. P(kPa) 

B. T(K) 

C. Hxs(%) 

D. Kp(T)  10⁸ . (The given function of T multiplied by 10⁸. When T = 500 K, the value in this column should be 91.113.) 

E. K_pP² 

F. ṅ₃. The rate (kmol/h) at which H₂ enters the reactor. 

G. ṅ₄. The rate (kmol/h) at which CO leaves the reactor. 

H. ṅ₅. The rate (kmol/h) at which H₂ leaves the reactor. 

I. ṅ₆. The rate (kmol/h) at which methanol leaves the reactor.

J. ṅ_tot. The total molar flow rate (kmol/h) of the reactor effluent. 

K. K_pc  10⁸ . 

The ratio y_M= (y_COy²H₂) multiplied by 10⁸. When the correct solution has been attained, this value should equal the one in Column E. 

L. K_pP² - K_pcP² . Column E–Column K, which equals zero for the correct solution. 

M. ṅ₁. The molar flow rate (kmol/h) of CO in the fresh feed. 

N. ṅ₂. The molar flow rate (kmol/h) of H₂ in the fresh feed. 

O. V̇_rec(SCMH). The flow rate of the recycle stream in m³ (STP)/h.

When the correct formulas have been entered, the value in Column I should be varied until the value in Column L equals 0. 

Run the program for the following nine conditions (three of which are the same): 

• T = 500 K, H_xs = 5%, and P = 1000 kPa, 5000 kPa, and 10,000 kPa. 

• P = 5000 kPa, H_xs = 5%, and T = 400 K, 500 K, and 600 K. 

• T = 500 K, P = 5000 kPa, and Hxs = 0%, 5%, and 10%. 

Summarize the effects of reactor pressure, reactor temperature, and excess hydrogen on the yield of methanol (kmol M produced per 100 kmol CO fed to the reactor). 

(c) You should find that the methanol yield increases with increasing pressure and decreasing temperature. What cost is associated with increasing the pressure? 

(d) Why might the yield be much lower than the calculated value if the temperature is too low? 

(e) If you actually ran the reaction at the given conditions and analyzed the reactor effluent, why might the spreadsheet values in Columns F–M be significantly different from the measured values of these quantities? (Give several reasons, including assumptions made in obtaining the spreadsheet values.) 

Transcribed Image Text:

T(K) 473 350 335 315 300 Pgauge (atm) 1.00 0.272 0.111 -0.097 -0.224 Pure NO2