The nodal period of a satellite in a circular orbit of radius a and inclination i about the Earth is given by

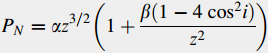
and the angular frequency of precession about the Earth€™s polar axis is given by

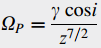
where z = (a/a_e) and a_e is the Earth€™s equatorial radius, 6378.160 km. The coefficients in the equations are

α = 5069.3s

β = 1.62395 x 10^-3

γ = 2.01280 x 10^-6

The orbit of the Envisat satellite is circular, with z = 1.122 51 and i = 98.52°.
(i) Show that the orbit is sun-synchronous.
(ii) The orbit is an exactly repeating orbit with a revisit interval of 35 days. Calculate the number of orbits that the satellite makes around the Earth in this period.
(iii) If the spacing of adjacent southbound tracks is Δl in longitude, show that if the track passes through longitude zero at the equator on day zero, it will pass through longitude +11Δl at the equator after approximately one day (the plus sign indicates that this longitude is east of the original longitude) and through longitude €“Δl on the equator on day 3.

Transcribed Image Text:

B(1 – 4 cos?i) 1+ az3/2 PN = az" z2 y cosi z7/2 Op