Question: a. A disk of mass M and radius R has a hole of radius r centered on the axis. Calculate the moment of inertia of

a. A disk of mass M and radius R has a hole of radius r centered on the axis. Calculate the moment of inertia of the disk.
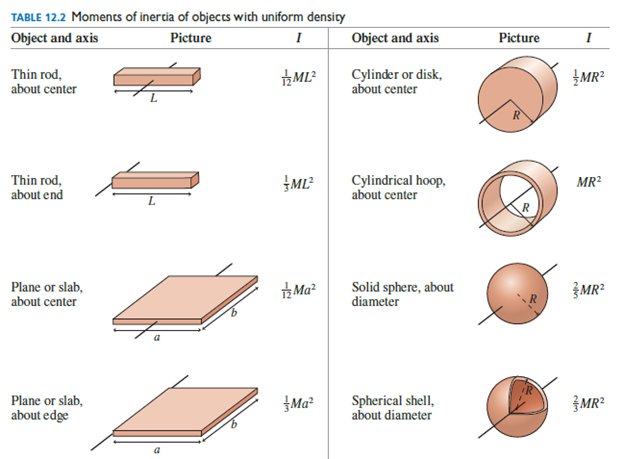
b. Confirm that your answer agrees with Table 12.2 when r = 0 and when r = R.

TABLE 12.2 Moments of inertia of objects wich uniform density Object and axis Picture Picture Object and axis ĮMR? Thin c. A 4.0-cm-diameter disk with a 3.0-cm-diameter hole rolls down a 50-cm-long, 20° ramp. What is its speed at the bottom? What percent is this of the speed of a particle sliding down a frictionless ramp?

TABLE 12.2 Moments of inertia of objects wich uniform density Object and axis Picture Picture Object and axis MR? Thin rod, about center ML? Cylinder or disk, about center Thin rod, about end ML? Cylindrical hoop, about center MR? Solid sphere, about diameter Plane or slab, about center Ma? MR? Plane or slab, about edge Ma Spherical shell, about diameter MR?

Step by Step Solution

★★★★★

3.41 Rating (170 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Visualize Solve We solve this problem by dividing the disk between radii r 1 and r 2 into narrow rin... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Physics Scientists and Engineers Questions!

(1) True or false: (a) Angular velocity and linear velocity have the same dimensions. (b) All parts of a rotating wheel must have the same angular velocity. (c) All parts of a rotating wheel must...

(a) A disk of mass M and radius R is held up by a massless string, as shown in Fig. The surface of the disk is frictionless. What is the tension in the string? What is the normal force per unit...

A disk of mass M and radius R rolls without slipping down a plane inclined from the horizontal by an angle a. The disk has short weightless axle of negligible radius. From this axis is suspended a...

A thin, flat, uniform disk has mass M and radius R_ A circular hole of radius R/4, centered at a point R/2 from the disk's center, is then punched in the disk. (a) Find the moment of inertia of the...

A disk of mass MM and radius RR has a hole of radius rr centered on the axis. Part A Calculate the moment of inertia of the disk. Express your answer in terms of the variables MM , RR , and rr . View...

A disk of mass M and radius R has a hole of radius r centered on the axis.Calculate the moment of inertia of the disk. Express your answer in terms of the variables M , R , and r . A 4 . 9 - cm -...

A disk of mass MM and radius RR has a hole of radius rr centered on the axis.Calculate the moment of inertia of the disk. Express your answer in terms of the variables MM , RR , and r A 4 . 9 - cmcm...

Uhapter iz Rotational Motion II: Moment of Inertia (Composite Systems) In the previous lab we examined the concepts mo tion rotating about a xed axis of a platform which we approximated as a rod as...

I need some guidance on how to do questions 1-6. This seems straightforward, but I just want some clarification on these listed questions. 1. (3 pts) Moment of Inertia. Consider a uniform thin rod of...

1. (3 pts) Moment of Inertia. Consider a uniform thin rod of mass M and length & but pivoted about an axis which can be anywhere along the rod's length. Call the distance from the left end of the rod...

On January 1, 20X1, Veldon Co., a U.S. corporation with the U.S. dollar as its functional currency, established Malont Co. as a subsidiary. Malont is located in the country of Sorania, and its...

A manufacturing company produces two types of products, A and B, each requiring a different amount of time and resources. The company has a total of 800 hours of labor and 2000 units of raw materials...

At the beginning of 2 0 2 4 , a construction company changed from the completed - contract method to the percentage - of - completion method for accounting purposes but not for tax purposes. Income...

Monthly rates of return on the shares of a particular common stock are independent of one another and normally distributed with a standard deviation of 1.7 A sample of 12 months is taken. (a) Find...

If a proton and an electron are released when they are 2.0 10 -10 m apart (a typical atomic distance), find the initial acceleration of each particle.

The electric force between two charged particles becomes weaker with increasing distance. Suppose instead that the electric force were independent of distance. In this case, would a charged comb...

You have a pure (24-karat) gold ring of mass 10.8 g. Gold has an atomic mass of 197 g/mol and an atomic number of 79. (a) How many protons are in the ring, and what is their total positive charge?...

SCENARIO3: The following table presents total retail sales in millions of dollars for the leading apparel companies over a two-year period in the past. APPAREL COMPANY Year 1 Year 2 Gap 1,159.0 962.0...

Mr. Agirich has provided the following information and ratios for the Aggie Farms 20X0 operations: Average Total Assets = $840,000 Average Total Liabilities = $395,000 Net Farm Income before taxes =...

Given that stock X has an expected return of 8 percent, which of the following statements are true? I. If its standard deviation is positive, then the return of stock X may sometimes be above 8...