According to Benford’s law (Exercise 15), the probability that the first digit of the amount of a randomly chosen invoice is an 8 or a 9 is 0.097. Suppose you examine randomly selected invoices from a vendor until you find one whose amount begins with an 8 or a 9.

a. How many invoices do you expect to examine before finding one that begins with an 8 or 9?

b. In fact, the first invoice you find with an amount that starts with an 8 or 9 is the 40th invoice. Does this result provide convincing evidence that the invoice amounts are not genuine? Calculate an appropriate probability to support your answer.

Exercise 15.

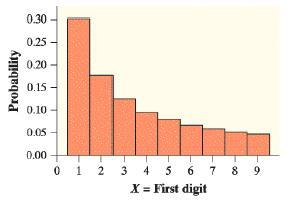
Exercise 9 described how the first digits of numbers in legitimate records often follow a model known as Benford’s law. Call the first digit of a randomly chosen legitimate record X for short. The probability distribution for X is shown here (note that a first digit can’t be 0). From Exercise 9, E(X) = 3.441. Find the standard deviation of X. Interpret this value.

Exercise 9.

Faked numbers in tax returns, invoices, or expense account claims often display patterns that aren’t present in legitimate records. Some patterns, like too many round numbers, are obvious and easily avoided by a clever crook. Others are more subtle. It is a striking fact that the first digits of numbers in legitimate records often follow a model known as Benford’s law. Call the first digit of a randomly chosen legitimate record X for short. The probability distribution for X is shown here (note that a first digit cannot be 0).

Transcribed Image Text:

First digit x; 1 2 4 5 6. 7 8 9 Probability p; 0.301 0.176 0.125 0.097 0.079 0.067 0.058 0.051 0.046