Examine how Benford’s law (Exercise 9) can be used to detect fraud.

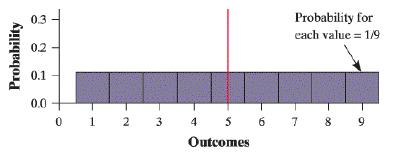
A not-so-clever employee decided to fake his monthly expense report. He believed that the first digits of his expense amounts should be equally likely to be any of the numbers from 1 to 9. In that case, the first digit Y of a randomly selected expense amount would have the probability distribution shown in the histogram.

a. What’s P(Y<6) ? According to Benford’s law (see Exercise 9), what proportion of first digits in the employee’s expense amounts should be greater than 6? How could this information be used to detect a fake expense report?

b. Explain why the mean of the random variable Y is located at the solid red line in the figure.

c. According to Benford’s law, the expected value of the first digit is μX=3.441 . Explain how this information could be used to detect a fake expense report.

Exercise 9.

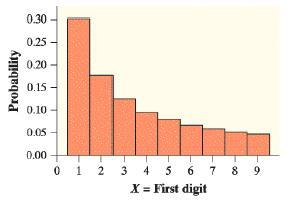
Faked numbers in tax returns, invoices, or expense account claims often display patterns that aren’t present in legitimate records. Some patterns, like too many round numbers, are obvious and easily avoided by a clever crook. Others are more subtle. It is a striking fact that the first digits of numbers in legitimate records often follow a model known as Benford’s law.4 Call the first digit of a randomly chosen legitimate record X for short. The probability distribution for X is shown here (note that a first digit cannot be 0).

Transcribed Image Text:

Probability for cach value = 1/9 0.3 0.2 2 - 0.1 0.0 0 1 2 3 4 5 6 7 8. 9. Outcomes Probability