A 24-in.-by-36-in. sheet of cardboard is folded in half to form a 24-in.-by-18-in. rectangle as shown in
Question:
A 24-in.-by-36-in. sheet of cardboard is folded in half to form a 24-in.-by-18-in. rectangle as shown in the accompanying figure. Then four congruent squares of side length x are cut from the corners of the folded rectangle. The sheet is unfolded, and the six tabs are folded up to form a box with sides and a lid.
a. Write a formula V(x) for the volume of the box.
b. Find the domain of V for the problem situation and graph V over this domain.
c. Use a graphical method to find the maximum volume and the value of x that gives it.
d. Confirm your result in part (c) analytically.
e. Find a value of x that yields a volume of 1120 in3.
f. Write a paragraph describing the issues that arise in part (b).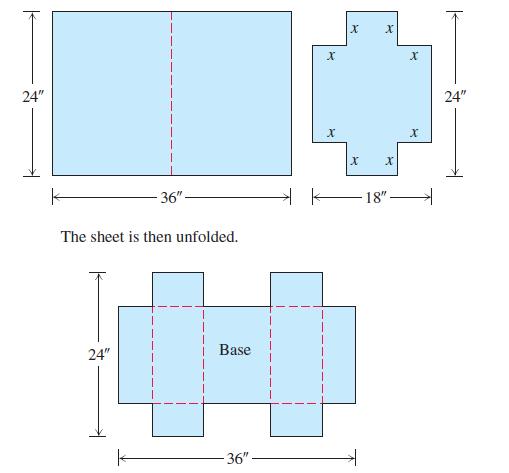
Step by Step Answer:

Thomas Calculus Early Transcendentals
ISBN: 9780321884077
13th Edition
Authors: Joel R Hass, Christopher E Heil, Maurice D Weir





