(a) Given a circular sector with radius L and central angle (see figure), show that the...
Question:
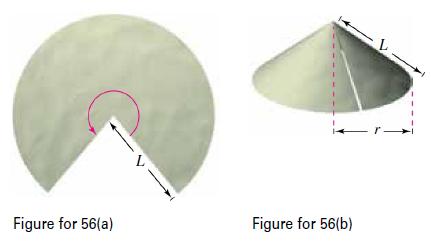
(a) Given a circular sector with radius L and central angle θ (see figure), show that the area of the sector is given by S = 1/2 L2θ.
(b) By joining the straight-line edges of the sector in part (a), a right circular cone is formed (see figure) and the lateral surface area of the cone is the same as the area of the sector. Show that the area is S = πrL, where r is the radius of the base of the cone.
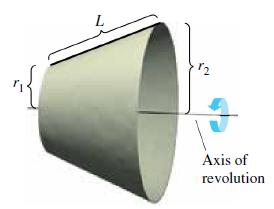
(c) Use the result of part (b) to verify that the formula for the lateral surface area of the frustum of a cone with slant height L and radii r1 and r2 (see figure) is S = π(r1 + r2)L.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
ANSWER a The area of a sector is given by A 12 r2 where r is the radius and is the central angle in ...View the full answer
Answered By
Collins Njuguna
I graduated from Maseno University with a Bachelor of Science in Applied Statistics. After graduation, I started tutoring students in mathematics. My experience in mathematics education is extensive and varied. I have taught a wide range of topics, including algebra, geometry, trigonometry, calculus, statistics, probability, and computer science. I have also worked with students of all ages and backgrounds, from elementary school to college.
My teaching method is based on the idea of hands-on learning. I believe that students learn best when they are actively engaged in the learning process, so I focus on giving students the tools they need to explore the material on their own. I also emphasize the importance of practice and review, as these are essential for mastering math concepts.
I have also developed several online and in-person courses on mathematics. My courses are designed to help students learn mathematics in an efficient and comprehensive way, and I use a variety of activities and exercises to ensure that my students are engaged and motivated.
Overall, my passion for mathematics and teaching has allowed me to be a successful tutor and educator in the field. I am confident that my experience will help your students master the mathematics they need to succeed.
0 Reviews
10+ Question Solved
Related Book For 
Calculus Of A Single Variable
ISBN: 9781337275361
11th Edition
Authors: Ron Larson, Bruce H. Edwards
Question Posted:
