Descartes’s method for finding tangents depends on the idea that, for many graphs, the tangent line at a given point is the unique line that intersects the graph at that point only. Apply his method to find an equation of the tangent line to the parabola y = x² at the point See the figure.

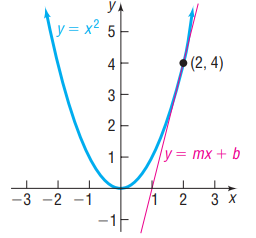
First, we know that the equation of the tangent line must be in the form y = mx + b. Using the fact that the point (2, 4) is on the line, we can solve for b in terms of m and get the equation y = mx + (4 - 2m).  Now we want to be the unique solution to the system 

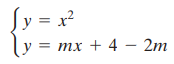
From this system, we get x² – mx + (2m – 4) = 0. By using the quadratic formula, we get 

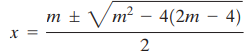
To obtain a unique solution for x, the two roots must be equal; in other words, the discriminant m² – 4(2m – 4) must be 0. Complete the work to get m, and write an equation of the tangent line.

\y = x2 (2, 4) 3 2 y = mx + b 1 2 3 x -3 -2 -1 3D ? 3D + 4 2m 2m