Green’s Theorem holds for a region R with any finite number of holes as long as the bounding curves are smooth, simple, and closed and we integrate over each component of the boundary in the direction that keeps R on our immediate left as we go along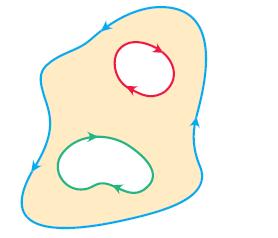

a. Let ƒ(x, y) = ln (x² + y²) and let C be the circle x² + y² = a². Evaluate the flux integral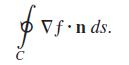

b. Let K be an arbitrary smooth, simple closed curve in the plane that does not pass through (0, 0). Use Green’s Theorem to show that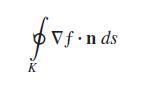

has two possible values, depending on whether (0, 0) lies inside K or outside K.