Just as x = cos u and y = sin u are identified with points (x, y) on the unit circle, the functions x = cosh u and y = sinh u are identified with points (x, y) on the right-hand branch of the unit hyperbola, x² - y² = 1.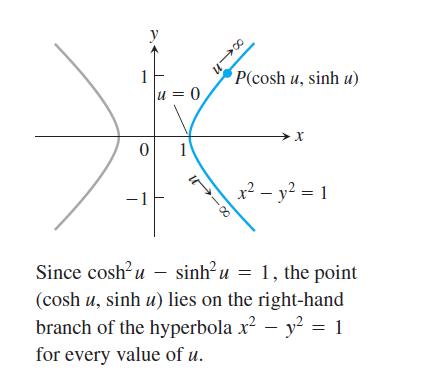

Another analogy between hyperbolic and circular functions is that the variable u in the coordinates (cosh u, sinh u) for the points of the right-hand branch of the hyperbola x² - y² = 1 is twice the area of the sector AOP pictured in the accompanying figure. To see why this is so, carry out the following steps.

a. Show that the area A(u) of sector AOP is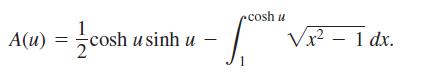

b. Differentiate both sides of the equation in part (a) with respect to u to show that

c. Solve this last equation for A(u). What is the value of A(0)? What is the value of the constant of integration C in your solution? With C determined, what does your solution say about the relationship of u to A(u)?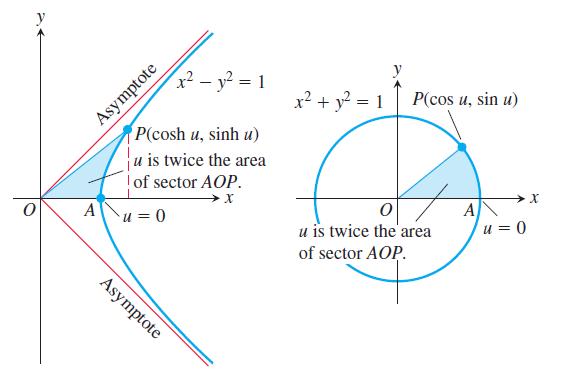

One of the analogies between hyperbolic and circular functions is revealed by these two diagrams (Exercises 86).

1 0 - 1 u=0 1 0111 4n P(cosh u, sinh u) X x - y = 1 Since coshu - sinh u = 1, the point (cosh u, sinh u) lies on the right-hand branch of the hyperbola x - y = 1 for every value of u.