Let F(x) = a x (t) dt for the specified function and interval [a, b].
Question:
Let F(x) = ∫axƒ(t) dt for the specified function ƒ and interval [a, b]. Use a CAS to perform the following steps and answer the questions posed.
a. Plot the functions ƒ and F together over [a, b].
b. Solve the equation F′(x) = 0. What can you see to be true about the graphs of ƒ and F at points where F′(x) = 0? Is your observation borne out by Part 1 of the Fundamental Theorem coupled with information provided by the first derivative? Explain your answer.
c. Over what intervals (approximately) is the function F increasing and decreasing? What is true about ƒ over those intervals?
d. Calculate the derivative ƒ′ and plot it together with F. What can you see to be true about the graph of F at points where ƒ′(x) = 0? Is your observation borne out by Part 1 of the Fundamental Theorem?
Explain your answer.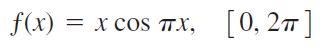
Step by Step Answer:

Thomas Calculus Early Transcendentals
ISBN: 9780321884077
13th Edition
Authors: Joel R Hass, Christopher E Heil, Maurice D Weir





