Let v(t, x, y, z) be a continuously differentiable vector field over the region D in space and let p(t, x, y, z) be a continuously differentiable scalar function. The variable t represents the time domain. The Law of Conservation of Mass asserts that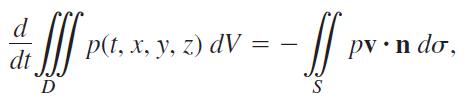

where S is the surface enclosing D.

a. Give a physical interpretation of the conservation of mass law if v is a velocity flow field and p represents the density of the fluid at point (x, y, z) at time t.

b. Use the Divergence Theorem and Leibniz’s Rule,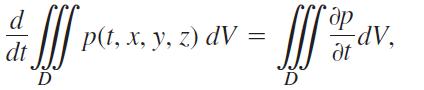

to show that the Law of Conservation of Mass is equivalent to the continuity equation,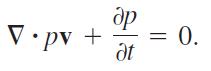

(In the first term ∇ · pv, the variable t is held fixed, and in the second term δp/δt, it is assumed that the point (x, y, z) in D is held fixed.)

fff PC D d dt p(t, x, y, z) dV= - 11 PV S pv.n do,