Suppose the curve in Exercise 1 is replaced by the conical helix r = a, z =

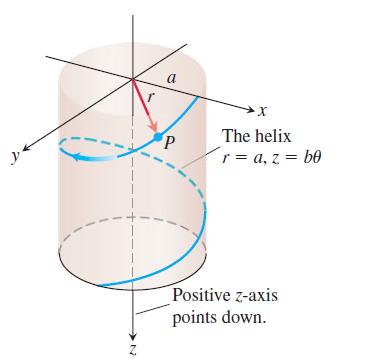
Suppose the curve in Exercise 1 is replaced by the conical helix r = aθ, z = bθ shown in the accompanying figure.

a. Express the angular velocity dθ/dt as a function of θ.

b. Express the distance the particle travels along the helix as a function of θ.

Data in Exercise 1

A frictionless particle P, starting from rest at time t = 0 at the point (a, 0, 0), slides down the helix

under the influence of gravity, as in the accompanying figure. The θ in this equation is the cylindrical coordinate θ and the helix is the curve r = a, z = bθ, θ ≥ 0, in cylindrical coordinates. We assume θ to be a differentiable function of t for the motion. The law of conservation of energy tells us that the particle’s speed after it has fallen straight down a distance z is √2gz, where g is the constant acceleration of gravity.

Transcribed Image Text:

N P Conical helix r = a0, z = b0 Cone z ār Positive z-axis points down. =