Taylors formula expresses the value of at x in terms of the values of and

Taylor’s formula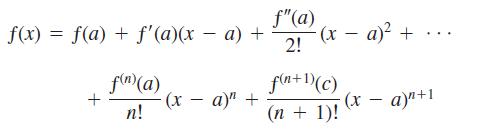

expresses the value of ƒ at x in terms of the values of ƒ and its derivatives at x = a. In numerical computations, we therefore need a to be a point where we know the values of ƒ and its derivatives. We also need a to be close enough to the values of ƒ we are interested in to make (x - a)ⁿ⁺¹ so small we can neglect the remainder.

What Taylor series would you choose to represent the function near the given value of x? Write out the first four nonzero terms of the series you choose.

cos x near x = 69

Transcribed Image Text:

f(x) = f(a) + f'(a)(x = a) + + f(n)(a) n! -(x - a)" + f"(a) 2! (x f(n+1)(c) (n + 1)! -(x a)² + - a) n+1