The interval of convergence of the geometric series

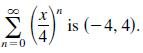
(a) Find the sum of the series when x = 5/2. Use a graphing utility to graph the first six terms of the sequence of partial sums and the horizontal line representing the sum of the series.

(b) Repeat part (a) for x = -5/2.

(c) Write a short paragraph comparing the rates of convergence of the partial sums with the sums of the series in parts(a) and (b). How do the plots of the partial sums differ as they converge toward the sum of the series?

(d) Given any positive real number M, there exists a positive integer N such that the partial sum

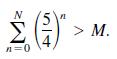
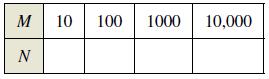
Use a graphing utility to complete the table.

Transcribed Image Text:

n=0 n is (-4,4).