The sine-integral function,

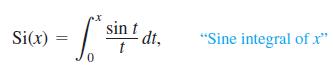
is one of the many functions in engineering whose formulas cannot be simplified. There is no elementary formula for the antiderivative of (sin t)/t. The values of Si(x), however, are readily estimated by numerical integration. Although the notation does not show it explicitly, the function being integrated is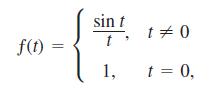

the continuous extension of (sin t) / t to the interval [0, x]. The function has derivatives of all orders at every point of its domain. Its graph is smooth, and you can expect good results from Simpson’s Rule.

a. Use the fact that |ƒ⁽⁴⁾| ≤ 1 on [0, π/2] to give an upper bound for the error that will occur if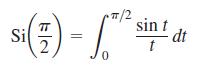

is estimated by Simpson’s Rule with n = 4.

b. Estimate Si(π/2) by Simpson’s Rule with n = 4.

c. Express the error bound you found in part (a) as a percentage of the value you found in part (b).

Si(x) - So 0 sin t t -dt, "Sine integral of x"