This exercise demonstrates a connection between the curl vector and rotations. Let B be a rigid body

Question:

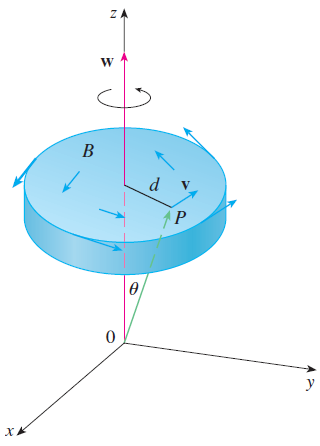
This exercise demonstrates a connection between the curl vector and rotations. Let B be a rigid body rotating about the z-axis. The rotation can be described by the vector w = k, where is the angular speed of B, that is, the tangential speed of any point P in B divided by the distance d from the axis of rotation. Let r = (x, y, z) be the position vector of P.
(a) By considering the angle θ in the figure, show that the velocity field of B is given by v = w x r.
(b) Show that v = -wy i + wx j.
(c) Show that curl v = 2w.

ZA B ө y хк