Use a CAS to perform the following steps for the function. a. Plot y = (x) over the interval (x 0 - 1/2) x

Use a CAS to perform the following steps for the function.

a. Plot y = ƒ(x) over the interval (x₀ - 1/2) ≤ x ≤ (x₀ + 3).

b. Holding x₀ fixed, the difference quotient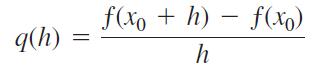

at x₀ becomes a function of the step size h. Enter this function into your CAS workspace.

c. Find the limit of q as h→ 0.

d. Define the secant lines y = ƒ(x₀) + q · (x - x₀) for h = 3, 2, and 1. Graph them together with ƒ and the tangent line over the interval in part (a).

ƒ(x) = x³ + 2x, x₀ = 0

q(h) = f(xo+h)-f(x) h