Use the Greek method described in Problem 53 to find an equation of the tangent line to the circle x2 + y2 €“ 4x + 6y + 4 = 0 at the point (3, 2ˆš2 - 3).

Data form problem 53

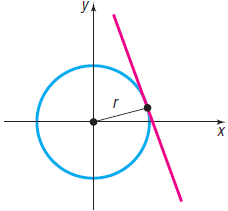
The Greek method for finding the equation of the tangent line to a circle uses the fact that at any point on a circle the lines containing the center and the tangent line are perpendicular (see Problem 52). Use this method to find an equation of the tangent line to the circle x² + y² = 9 at the point (1, 2ˆš2).

Data from problem 52

The tangent line to a circle may be defined as the line that intersects the circle in a single point, called the point of tangency. See the figure.