You will use a CAS to explore the osculating circle at a point P on a plane
Question:
You will use a CAS to explore the osculating circle at a point P on a plane curve where k ≠ 0. Use a CAS to perform the following steps:
a. Plot the plane curve given in parametric or function form over the specified interval to see what it looks like.
b. Calculate the curvature k of the curve at the given value t0 using the appropriate formula from Exercise 5 or 6. Use the parametrization x = t and y = ƒ(t) if the curve is given as a function y = ƒ(x).
c. Find the unit normal vector N at t0. Notice that the signs of the components of N depend on whether the unit tangent vector T is turning clockwise or counterclockwise at t = t0. (See Exercise 7.)
d. If C = ai + bj is the vector from the origin to the center (a, b) of the osculating circle, find the center C from the vector equation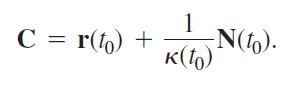
The point P(x0, y0) on the curve is given by the position vector r(t0).
e. Plot implicitly the equation (x - a)2 + (y - b)2 = 1/k2 of the osculating circle. Then plot the curve and osculating circle together. You may need to experiment with the size of the viewing window, but be sure the axes are equally scaled.
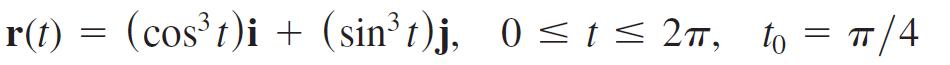
Exercise 6
a. Show that the curvature of a smooth curve r(t) = ƒ(t)i + g(t)j defined by twice-differentiable functions x = ƒ(t) and y = g(t) is given by the formula
The dots in the formula denote differentiation with respect to t, one derivative for each dot. Apply the formula to find the curvatures of the following curves.
b. r(t) = t i + (ln sin t)j, 0
c. r(t) = [tan-1 (sinh t)]i + (ln cosh t)j
Exercise 7
a. Show that n(t) = -g′(t)i + ƒ′(t)j and -n(t) = g′(t)i - ƒ′(t)j are both normal to the curve r(t) = ƒ(t)i + g(t)j at the point (ƒ(t), g(t)).
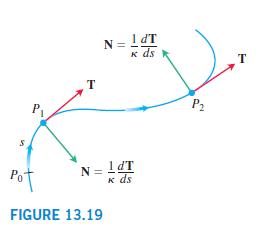
To obtain N for a particular plane curve, we can choose the one of n or -n from part (a) that points toward the concave side of the curve, and make it into a unit vector. (See Figure 13.19.) Apply this method to find N for the following curves.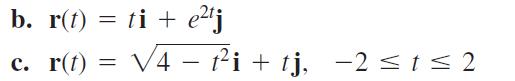
Step by Step Answer:

Thomas Calculus Early Transcendentals
ISBN: 9780321884077
13th Edition
Authors: Joel R Hass, Christopher E Heil, Maurice D Weir




