(a) Consider the design of an MMSE equalizer for a multi path channel whose output is of the form

y(t) = A d(t) + b A d(t - T_m) + n(t)

where the second term is a multi path component and the third term is noise independent of the data, d(t). Assume d(t) is a random (coin-toss) binary sequence with auto correlation function R_dd (Ï„) = Λ(Ï„/T). Let the noise have a low pass-RC-filtered spectrum with 3-dB cutoff frequency f₃ = 1/T so that the noise power spectral density is

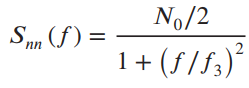
where N₀ / 2 is the two-sided power spectral density at the low pass filter input. Let the tap spacing be Δ = T_m = T. Express the matrix [R_yy] in terms of the signal-to-noise ratio E_d / N₀ = A²T / N₀.

(b) Obtain the optimum tap weights for a three-tap MMSE equalizer and at a signal-to-noise ratio of 10 dB.
(c) Find an expression for the MMSE.

No/2 .(f) = - 1 + (f/f,)* Sun Snn