A random process is composed of sample functions of the form

where n(t) is a wide-sense stationary random process with the auto correlation function R_n(Ï„), and n_k = n(kT_s).

(a) If T_s is chosen to satisfy

R_n(kT_s) = 0, k = 1,2,..

so that the samples n_k = n(kT_s) are orthogonal, use Equation (7.35) to show that the power spectral density of x(t) is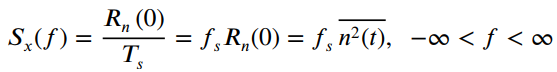 

(b) If x(t) is passed through a filter with impulse response h(t) and frequency response function H(f), show that the power spectral density of the output random process, y(t), is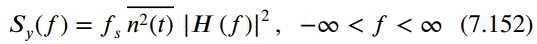 

0 0 - T ) = , - T) |x(t) = n (t) k=-00 k=-o R, (0) = f,R(0) = f,n(t), - < < T. un S,(f) =