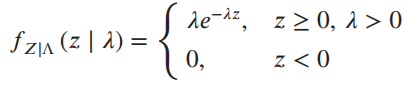
Question: Let an observed random variable Z depend on a parameter λ according to the conditional pdf The α priori pdf of λ is where β

Let an observed random variable Z depend on a parameter λ according to the conditional pdf z > 0, 1 > 0 z < 0 fZIA (z | 1) = 0,

The α priori pdf of λ is

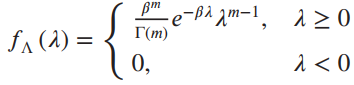
рт -е-ра ят-1, 120 fA (4) = Г(т) 0,

where β and m  are parameters and Γ(m) is the gamma function. Assume that m is a positive integer. 

(a) Find E{λ} and var {λ} before any observations are made; that is, find the mean and variance of λ using fΛ (λ).

(b) Assume one observation is made. Find fΛ|Z (λ|z1) and hence the minimum mean squared error (conditional-mean) estimate of λ and the variance of the estimate. Compare with part (a). Comment on the similarity of fΛ (λ) and fΛ|Z (λ|z1).

(c) Making use of part (b), find the posterior pdf of λ given two observations fΛ|Z (λ|z1, z2). Find the minimum mean-squared error estimate of λ based on two observations and its variance. Compare with parts (a) and (b), and comment.

(d) Generalize the preceding to the case in which K observations are used to estimate λ.

z > 0, 1 > 0 z < 0 fZIA (z | 1) = 0, -- -1, 120 fA (4) = () 0,

Step by Step Solution

★★★★★

3.43 Rating (169 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

a The characteristic function is found and used to obtain the moments By definition To integrate not... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Principles Communications Systems Questions!

Q:

An observed random process {x(n)} consists of the sum of an AR(p) process of the form And a white noise process {?(n)} with variance ?2?. The random process {v(n)} is also white with variance ?2v....

Q:

Given two independent, wide-sense stationary random processes X(t) and Y(t) with auto correlation functions R x () and R Y (), respectively. (a) Show that the auto correlation function R Z () of...

Q:

Let a random variable Z be defined in terms of three independent random variables as Z = 2X 1 + 4X 2 + 3X 3 , where the means of X 1 , X 2 , and X 3 are -1, 5, and -2, respectively, and their...

Q:

Probability and Statistics - Problem Set c Keith M. Chugg October 2, 2015 1 Preliminaries, Combinatorics, Set Probability 1.1. A number of bats are in a cave. 2 bats can see out of their left eye. 3...

Q:

Algorithms in Artificial Intelligence (or, the old name: Introduction to Algorithmic Decision Making) Part 1 Based on slides by David Sarne and Lirong Xia Course Tentative Schedule Introduction...

Q:

MATH S350 TMA 01 Hints Question 1 Let A and B be the event that water is contaminated with excessive amount of pollutant A and pollutatnt B respectively. Remarks: 1. Half of those communities whose...

Q:

Exercises Chapter 2 2.1 Marginal and conditional probability: The social mobility data from Section 2.5 gives a joint probability distribution on (Y1 , Y2 )= (father's occupation, son's occupation)....

Q:

1. Calculate the sample size needed given these factors: one-tailed t-test with two independent groups of equal size small effect size (see Piasta, S.B., & Justice, L.M., 2010) alpha =.05 beta = .2...

Q:

a) What is the difference between the likelihood density function and the a posteriori density function. b) Let x=s+n, where the observed random variable is 'x'. 's' is a random parameter independent...

Q:

Let x=s+n, where the observed random variable is 'x'. 's' is a random parameter independent of the added random noise 'n'. The probability density of n' is given by p(n) = 2 e-z (n-) u(n - 1) and the...

Q:

By now you know that monopoly power occurs in most markets. You also know that in some cases, a regulated monopoly produces a better outcome than competition. Yet an inappropriate use of monopoly...

Q:

Why do you think assembly in the consumer electronics industry is performed by third parties, whereas assembly in the auto industry is almost never outsourced?

Q:

2-3 A wholesale distributor of automobile supplies finds that the number of batteries of a given type he has sold per year during the past seven years and the corresponding values of a certain...

Q:

1. What is a subsidiary?

Q:

The transfer function relating the blood pressure of a patient to the infusion rate of a blood pressure drug is given by where θ 1 = 30 s, θ 2 = 45 s, and Ï 1 = 40 s....

Q:

Consider the transfer function (a) What are the gain, time delay, time constants, poles, and zeros of G(s)? (b) Will the step response of this transfer function exhibit (i) inverse response or (ii)...

Q:

composition analyzer is used to measure the concentration of a pollutant in a wastewater stream. The relationship between the measured composition Cm and the actual composition C is given by the...

Q:

The coach of the Red Shirts, a Multi-dimensional League Baseball team, is recruiting new players. To do so, she is conducting a home run competition. Each batter gets 100 tries to hit an identically...

Q:

Can someone explain how to do #16 only please? Unsure of how to get those numbers and if you can, provide formulas! Thanks in advance! 52.4015=12 P3=12.035.15=57.22 P0=57.22(1.12)3=40.73 .075=P65...

Q:

Taylor United is considering overhauling its equipment to meet increased demand for its product The cost of equipment overhaul is $ 3 . 9 8 million, plus $ 2 2 6 , 0 3 0 . 0 0 in installation costs....