Repeat Problem 9.8 using the Whitney-Nuismer point stress criterion and the parameter \(d_{0}=1 \mathrm{~mm}\).

Problem 9.8

Use the Whitney-Nuismer average stress criterion to estimate the allowable internal pressure for Problem 9.5 if the unnotched tensile strength of the material is \(\sigma_{0}=1500 \mathrm{MPa}\) and the parameter \(a_{0}=3 \mathrm{~mm}\).

Problem 9.5

As in Problem 9.4, assume that the tube in Figure 9.8 is subjected only to an internal pressure and neglect the longitudinal stress.

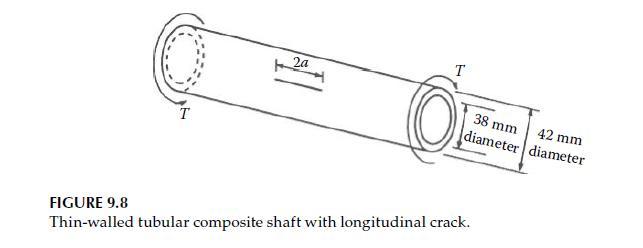
a. Determine the allowable internal pressure, \(p\), if the crack length in Figure 9.8 is \(2 a=10 \mathrm{~mm}\). Use the same dimensions and fracture toughness values that were given in Problem 9.4.

Problem 9.4.

The tube shown in Figure 9.8 is subjected to an internal pressure, \(p=5 \mathrm{MPa}\), instead of a torque. Neglecting the stress along the longitudinal axis of the tube, and assuming that the mode I fracture toughness is \(K_{\mathrm{Ic}}=10 \mathrm{MPa} \mathrm{m}^{1 / 2}\), determine the critical crack size.

b. Using the yield stress from Problem 9.3 and ignoring the crack, compare the answer from part (a) of this problem with the allowable internal pressure based on the maximum shear stress criterion for yielding.

Problem 9.3

a. Determine the allowable torque, \(T\), if the crack length for the shaft in Figure 9.8 is \(2 a=10 \mathrm{~mm}\). Use the same dimensions and fracture toughness values that were given in Problem 9.2.

b. If the uniaxial yield stress for the shaft material is \(Y=1200 \mathrm{MPa}\), and the crack is ignored, compare the answer from part (a) with the allowable torque based on the maximum shear stress criterion for yielding.

Problem 9.2

The thin-walled tubular shaft shown in Figure 9.8 is made of a randomly oriented, short-fiber-reinforced metal matrix composite. The shaft has a longitudinal through-thickness crack of length \(2 a\) and is subjected to a torque \(T=1 \mathrm{KN} \mathrm{m}\). If the mode II fracture toughness of the composite is \(K_{\text {IIc }}=40 \mathrm{MPa} \mathrm{m}^{1 / 2}\), determine the critical crack size for self-sustaining crack growth.

Transcribed Image Text:

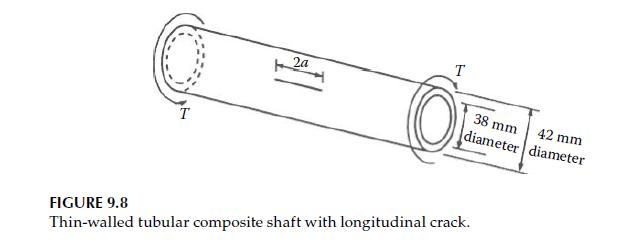
T 2a 38 mm. 42 mm diameter diameter FIGURE 9.8 Thin-walled tubular composite shaft with longitudinal crack.