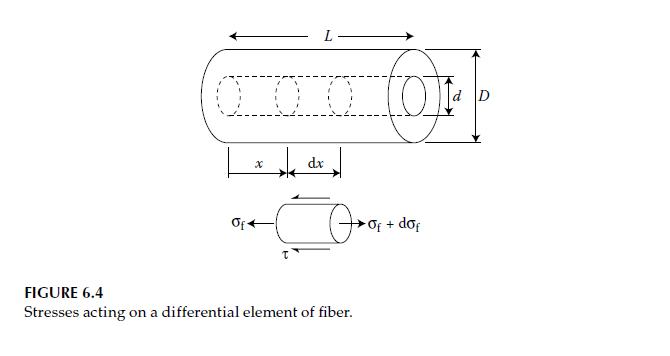
The RVE for an aligned discontinuous fiber composite without matrix material at its ends is shown in Figure 6.4. Assume that when the RVE is loaded along the fiber direction, the interfacial shear stress distribution is given by

\[\tau=\frac{2 \tau_{\max }}{L}\left(\frac{L}{2}-x\right)\]

and the fiber tensile stress is given by

\[\sigma_{\mathrm{f}}=\frac{4 \sigma_{\mathrm{fmax}} x(L-x)}{L^{2}}\]

where \(L=\) fiber length, \(x=\) distance from the left end of RVE, \(\tau_{\max }=\) maximum interfacial shear stress, and \(\sigma_{\mathrm{fmax}}=\) maximum fiber tensile normal stress.

a. Sketch the distributions of \(\tau\) and \(\sigma_{\mathrm{f}}\) along the length of the fiber.

b. Neglecting the stress transmitted across the ends of the fiber, derive the relationship between \(\tau_{\max }\) and \(\sigma_{\text {fmax }}\).

c. If the interfacial shear strength is about the same as the fiber tensile strength, and the fiber aspect ratio \(L / d\) is very large (say \(L / d>1000\) ), will the most likely mode of failure be interfacial shear failure or fiber tensile failure?

Transcribed Image Text:

Of x dx FIGURE 6.4 Stresses acting on a differential element of fiber. Of + dof d D