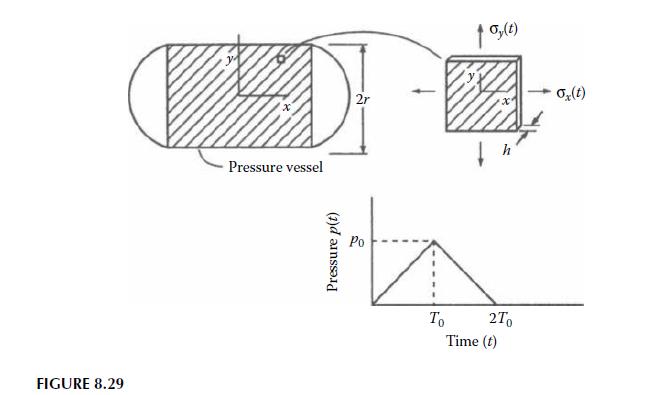
The time-dependent axial stress, \(\sigma_{x}(t)\) and the time-dependent circumferential stress, \(\sigma_{y}(t)\) in the wall of the filament-wound, thin-walled composite pressure vessel shown in Figure 8.29 are caused by the internal pressure \(p(t)\), where \(t\) is time. The required dimensions of the vessel are the wall thickness \(h\) and the mean radius \(r\). Note that \(x\) and \(y\) are not the principal material axes, but, rather, are the longitudinal and transverse axes for the vessel. The variation of \(p(t)\) with time is also shown in Figure 8.29. If the creep compliances associated with the \(x\) and \(y\) axes are given in contracted notation by

\[\bar{S}_{i j}(t)=\bar{E}_{i j}+\bar{F}_{i j} t, \quad i, j=1,2, \ldots, 6\]

where \(\bar{E}_{i j}\) and \(\bar{F}_{i j}\) are material constants, determine all the time-dependent strains along the \(x\) and \(y\) axes for \(t>2 T_{0}\). Answers should be given in terms of \(p_{0}, r, h, T_{0}, t\), and the individual \(\bar{E}_{i j}\) and \(\bar{F}_{i j}\).

Transcribed Image Text:

FIGURE 8.29 Pressure vessel Pressure p(t) Po 2r To 2T Time (t) 10,(t) Ox(t)