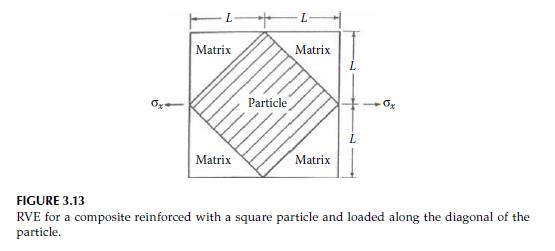
Using the result from Problem 3.9, determine the effective Young's modulus, \(E_{x}\), for the RVE shown in Figure 3.13. In Figure 3.13, the reinforcing particle has a square cross section and is oriented as shown. For a particle having a Young's modulus \(E_{\mathrm{p}}=10 \times 10^{6} \mathrm{psi}(68.95 \mathrm{GPa})\) and a matrix having a Young's modulus \(E_{\mathrm{m}}=0.5 \times 10^{6} \mathrm{psi}(3.45 \mathrm{GPa})\), determine the value of \(E_{x}\) and compare with the values from the rule of mixtures Equation 3.27 and the inverse rule of mixtures Equation 3.40.

Problem 3.9

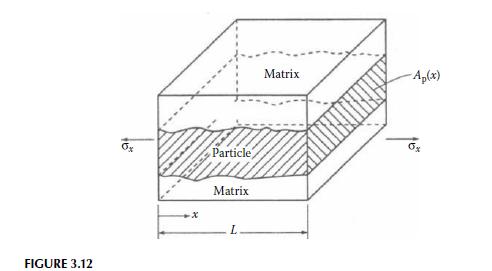
An RVE from a particle-reinforced composite is shown in Figure 3.12. The particle has a cross-sectional area \(A_{\mathrm{p}}(x)\) that varies with the distance \(x\), and the stresses and strains in particle and matrix materials also vary with \(x\). Find the expression for the effective Young's modulus of the composite, \(E_{x}\) along the \(x\) direction. The answer should be left in terms of an integral involving the length, \(L\); the particle modulus, \(E_{\mathrm{p}}\); the matrix modulus, \(E_{\mathrm{m}} ;\) and the particle area fraction \(a_{\mathrm{p}}(x)=A_{\mathrm{p}}(x) / A_{\mathrm{c}}\), where \(A_{\mathrm{c}}\) is the total composite crosssectional area. Assume that both the particle and the matrix are isotropic.

Transcribed Image Text:

FIGURE 3.12 0x Particle x Matrix L Matrix -Ap(x)