This exercise has to do with whether convergence of all moments, that is, (16.29), implies convergence in distribution.

(a) Find a counterexample such that a sequence of pdf’s, fn, n = 1, 2, . . .

share the same moments with another pdf, f , that is,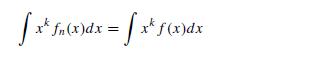

for every positive integer k (and every n), but fn(x) = f (x) almost surely.

(b) Construct a sequence of distributions, Fn, such that

as n→∞for every positive integer k, but Fn does not converge weakly to F.

Transcribed Image Text:

xp(x) ** [ = xp(x)xx [