This exercise provides a very simple special case of the Gibbs sampler that was considered by Casella and George (1992). Let the state-space be S = {0, 1}2. A probability distribution π defined over S has π({(i, j )}) =

πij , i, j = 0, 1. The Gibbs sampler draws θ = (θ1, θ2) according to the following:

1. Given θ2 = j, draw θ1 such that

π1(0|j) = P(θ1 = 0|θ2 = j) = π0j

π·j

, π1(1|j) = P(θ1 = 1|θ2 = j) = π1j

π·j

, where π·j = π1j + π2j , j = 0, 1.

2. Given θ1 = i, draw θ2 such that

π2(0|i)) = P(θ2 = 0|θ1 = i) = πi0 πi·
, π2(1|i) = P(θ2 = 1|θ1 = i) = πi1 πi·
, where πi· = πi0 + πi1, i = 0, 1.
Given the initial value θ0 = (θ01, θ02), let θt = (θt1, θt2)
be the drawn of iteration t , t = 1, 2, . . . .
(i) Show that θt is a (discrete state-space) Markov chain with transition probability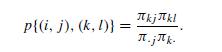

ii) Show that π is the stationary distribution of the chain.
(iii) Using the result of Section 10.2 (in particular, Theorem 10.2), find simple sufficient conditions (or condition) for the convergence of the Markov chain. Are the sufficient conditions (or condition) that you find also necessary, and why? [Hint: The results of Section 10.2 apply to vector-valued discrete space Markov chains in obvious ways. Or, if you wish, you may consider a scalar chain that assumes values in correspondence with θt (e.g., ψt = 10θt1+θt2). This is always possible for a discrete state-space chain.]

Transcribed Image Text:

p{(i, j), (k, l)}= kjkl