Question: 1. Let X(t) : t 0 be a continuous-time Markov chain with state space S. Show that for i, j S and t

1. Let

X(t) : t ≥ 0


be a continuous-time Markov chain with state space S. Show that for i, j ∈ S and t ≥ 0,

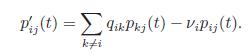
P(t)=ikPky (t) - Vipij(t). kpi

In other words, prove Kolmogorov’s backward equations.

P(t)=ikPky (t) - Vipij(t). kpi

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Probability And Stochastic Modeling Questions!

Q:

.Answer the following questions given below. 1 Analytics of the Solow Model In the Solow economy, people consume a good that firms produce with technology Y = Af (K, L), where A is TFP (which we...

Q:

Hi, please can you answer this Stochastic Processes question for me, thank you. 4. (a) Boy Tom is always in one of three states: eat, play and sleep. He eats on average for 20 minutes at a time;...

Q:

Portray in words what transforms you would have to make to your execution to some degree (a) to accomplish this and remark on the benefits and detriments of this thought.You are approached to compose...

Q:

1. Let X = (Xn, n 0) be an irreducible Markov chain with state space V and transition matrix P = (Pu,v)u,v2V . (a) (3 marks) Show that the process Y = ((Xn, Xn+1), n 0) is a Markov chain with state...

Q:

2. Let {X (15),): 2 0} be a continuoustime Markov chain with state space S = {0,1,2} and the following generator 2 1 1 q = 2 3 1 1 2 3 Determine the following quantities: (a) the distribution of the...

Q:

2. Let {X (15),): 2 0} be a continuoustime Markov chain with state space S = {0,1,2} and the following generator 2 1 1 q = 2 3 1 1 2 3 Determine the following quantities: (a) the distribution of the...

Q:

2. Let {X (15),): 2 0} be a continuoustime Markov chain with state space S = {0,1,2} and the following generator 2 1 1 q = 2 3 1 1 2 3 Determine the following quantities: (a) the distribution of the...

Q:

1. Let $ X(t): t 0 % be a continuous-time Markov chain with state space S. Show that for i, j S and t 0, p7 ij (t) = . k,=i qikpkj (t) ipij (t). In other words, prove Kolmogorovs backward...

Q:

(Continuous-time first step analysis) Let {X(t), t 2 0} be a continuous-time Markov chain with state space S and generator q = (qry). Let A = {x ( S : qxx = 0} be the set of absorbing states. Assume...

Q:

(Continuous-time first step analysis) Let {X(t), t 2 0} be a continuous-time Markov chain with state space S and generator q = (qry). Let A = {x ( S : qxx = 0} be the set of absorbing states. Assume...

Q:

KEW Enterprises began operations in January 2012 to manufacture a hand sanitizer that promised to be more effective and gentler on the skin than existing products. Family members, one of whom was...

Q:

Suppose you are selling a piece of furniture to a friend who cant afford to pay you upfront but offers to pay you in monthly installments for the next year. What information do you need to calculate...

Q:

The estimate life of a building that has been depreciated for 3 0 years of an originally estimated life of 5 0 yearsnhas been revised to a remaining life of 1 0 years. Based on this information the...

Q:

Using the data in BE7-11, prepare the adjusting entries required on July 31 for Southco Limited. In BE7-11 At July 31, Southco Limited had an unadjusted cash balance of $16,320. An examination of the...