A number is called a median for a continuous r.v. X if P(X ) = 1/2.
Question:
A number μ is called a median for a continuous r.v. X if P(X μ) = 1/2.
(a) Show that for any symmetric distribution, its median, center of symmetry, and mean (if it exists) coincide. (Advice: First, switch to the r.v. X −s, where X is the r.v. in hand and s is its center of symmetry.)
(b) Find a median for the exponential distribution, and for the distribution in Exercise 1.
Exercise 1
Let a r.v. X have the density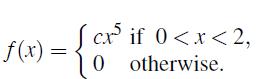
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





