(a) Which distribution below would you call symmetric, and which “skewed”?

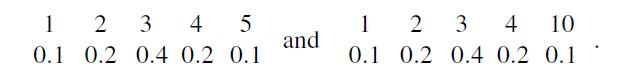
(b) Rigorously speaking, the distribution of a discrete r.v. X is said to be symmetric if for a number s called a center of symmetry, P(X = s+x) = P(X = s−x) for any x > 0. Explain the sense of this definition, and illustrate it by the example above. Explain why we may consider all x’s in this definition.

(c) Does the center of symmetry have to equal one of the values of the r.v.?

(d) Compare the two following distributions: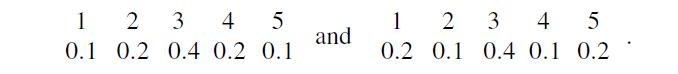

What is the difference? Are both distributions symmetric? For which distribution does the “dispersion” or “variation” of values seem to you larger?