According to the order, the rated nominal capacitance of condensers in a large delivery should be (300
Question:
According to the order, the rated nominal capacitance of condensers in a large delivery should be \(300 \mu F\). Their actual rated nominal capacitances are, however, random variables \(X\) with
\[E(X)=300 \text { and } \operatorname{Var}(X)=144\]
(1) By means of Chebyshev's inequality determine an upper bound for the probability of the event \(A\) that \(X\) does not differ from the rated nominal capacitance by more than \(5 \%\).
(2) Under the additional assumption that \(X\) is a continuous random variable with unimodal density and mode \(x_{m}=300\), solve (1) by means of the Gauss inequality (5.4).
(3) Determine the exact probability on condition that
\[X=N(300,144)\]
(4) A delivery contains 600 condensers. Their capacitances are independent and identically distributed as \(X\). The distribution of \(X\) has the same properties as stated under (2). By means of the Gauss inequality (5.4) give a lower bound for the probability that the arithmetic mean of the capacitances of the condensers in the delivery differs from \(E(X)=300\) by less than 0.01 .
Data from 5.4
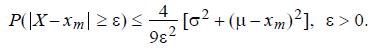
Step by Step Answer:

Applied Probability And Stochastic Processes
ISBN: 9780367658496
2nd Edition
Authors: Frank Beichelt





