Consider the two-unit system with standby redundancy discussed in example 9.5 a) on condition that the lifetimes of the units are exponential with respective parameters \(\lambda_{1}\) and \(\lambda_{2}\). The other model assumptions listed in example 9.5 remain valid.

Model the system by a Markov chain and draw the transition graph.

Data from Example 9.5

............................

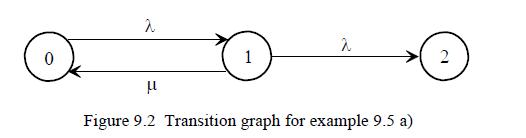
Transcribed Image Text:

Example 9.5 (two-unit redundant system, standby redundancy) A system consists of two identical units. The system is available if and only if at least one of its units is available. If both units are available, then one of them is in standby redundancy (cold redundancy), that is, in this state it does not age and cannot fail. After the failure of a unit, the other one (if available) is immediately switched from the redundancy state to the operating state and the replacement of the failed unit begins. The replaced unit becomes the standby unit if the other unit is still operating. Otherwise it immediately resumes its work. The lifetimes and replacement times of the units are independent random variables, identically distributed as L and Z, respectively. L and Z are assum- ed to be exponentially distributed with respective parameters and . Let Ls denote the system lifetime, i.e. the random time to a system failure. A system failure occurs when a unit fails whilst the other unit is being replaced. A Markov chain {X(t), t>0} with state space Z = {0,1,2} is introduced in the following way: X(t) = if i units are unavailable at time t. Let Y; be the unconditional sojourn time of the system in state i and Yi; be the conditional sojourn time of the system in state i given that the system makes a transition from state i into state j. From state 0, the system can only