Let (B_{t}=left(b_{t}, beta_{t} ight)) be a (mathrm{BM}^{2}). Solve the (mathrm{SDE}) [X_{t}=x+b int_{0}^{t} X_{s} d s+sigma_{1} int_{0}^{t} X_{s}
Question:
Let \(B_{t}=\left(b_{t}, \beta_{t}\right)\) be a \(\mathrm{BM}^{2}\). Solve the \(\mathrm{SDE}\)
\[X_{t}=x+b \int_{0}^{t} X_{s} d s+\sigma_{1} \int_{0}^{t} X_{s} d b_{s}+\sigma_{2} \int_{0}^{t} X_{s} d \beta_{s}\]
with \(x, b \in \mathbb{R}\) and \(\sigma_{1}, \sigma_{2}>0\).
Rewrite the SDE using the result of Problem 19.3 and then apply Example 21.4.
Data From 19.3 Problem
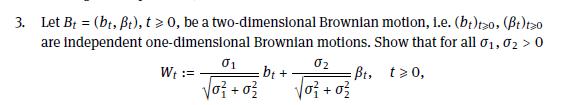
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Brownian Motion A Guide To Random Processes And Stochastic Calculus De Gruyter Textbook
ISBN: 9783110741254
3rd Edition
Authors: René L. Schilling, Björn Böttcher
Question Posted:





