Let X 1 and X 2 have the -distributions with the common scale parameter a = 1
Question:
Let X1 and X2 have the Γ-distributions with the common scale parameter a = 1 and essential parameters ν1 and ν2, respectively. Let S = X1+X2. Given S = s, the r.v. X1 takes on values from [0, s].
(a) Using formula (5.1.5), prove that the conditional density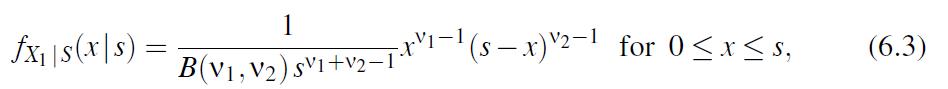
where the Beta-function B(ν1, ν2) is defined in (4.2.3)-(4.2.4).
Prove that the corresponding conditional density of the r.v. Y = 1/s X1 which takes on values from [0,1], is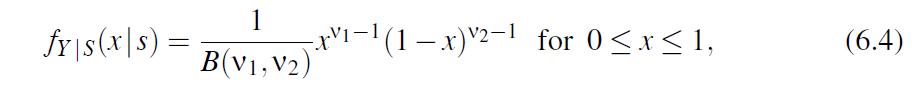
and does not depend on s. The last distribution is referred to as the Beta-distribution.
(b) Which distribution are we dealing with in (6.4) when ν1 = ν2 = 1. Connect this fact.
(c) Proceeding from (6.4), find the conditional distribution of Y and E{Y |S} for ν1 = ν and ν2 = 1. Does it grow when ν is increasing? To what does this distribution and E{Y |S}converge as ν→∞. Give a common-sense interpretation.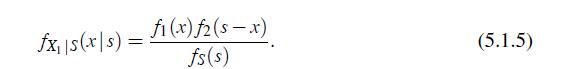
Step by Step Answer:






