Proceeding from Theorem 9, justify rigorously the ergodicity property for chains in Examples 1.2-1,2,3. Examples 1.2 A
Question:
Proceeding from Theorem 9, justify rigorously the ergodicity property for chains in Examples 1.2-1,2,3.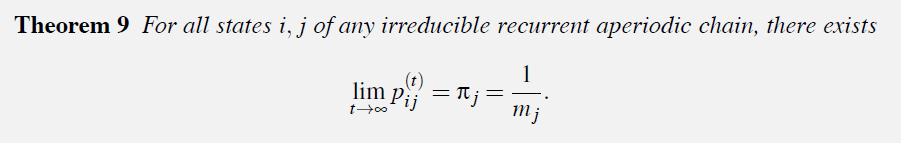
Examples 1.2
A police department provides daily reports on traffic accidents in a particular area. The intensity of daily accidents depends on weather conditions. The department distinguishes three types: normal, rainy, and icy-road conditions, which corresponds to three states we will label 0,1, 2. If the time period under consideration is not long, we may assume that the transition probabilities do not depend on time. For instance, for a soft winter, the transition matrix may look like
Since among pii’s (the probabilities of staying in the same state as on the previous day), the probability p00 = 0.6 is the largest, the normal conditions appear to be the most stable.
Examples 2.3
Assume that the process may move from state i =0,1,2, ... either to state i + 1 with probability p, or to state 0 with probability q = 1− p. In other words, the process either “moves up” by one step, or “falls to the bottom” and starts from the state 0. Assume, for example, that we are dealing with repeated independent trials, and p is the probability of success at each trial. We are interested in the number of consecutive successes, or in other words, we consider the length of the success run. At each step, the length mentioned may either increase by one or drop to zero.
(Suppose, for instance, for an investor, each day is either lucky or not with probabilities p and q, respectively, and the investor is interested in the length of the period of the capital growth.)
The transition matrix in this case is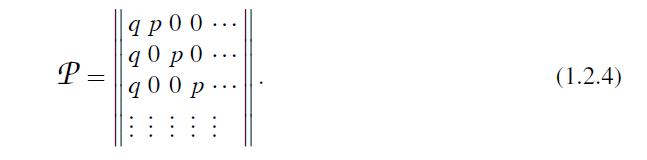
Step by Step Answer:






