Prove (20.20), i.e. show that (mathbb{E}left[B_{T}^{2 n} e^{-B_{T}^{2}} ight]=frac{(2 n-1) ! !}{sqrt{2 T+1}}left(frac{T}{2 T+1} ight)^{n}). Here, ((-1)
Question:
Prove (20.20), i.e. show that \(\mathbb{E}\left[B_{T}^{2 n} e^{-B_{T}^{2}}\right]=\frac{(2 n-1) ! !}{\sqrt{2 T+1}}\left(\frac{T}{2 T+1}\right)^{n}\). Here, \((-1) ! !:=1\), \((2 n-1) ! !=1 \cdot 3 \cdot \ldots \cdot(2 n-1)\), is the double factorial.
Data From Formula (20.20)
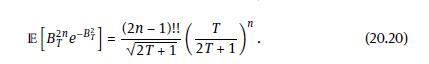
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Brownian Motion A Guide To Random Processes And Stochastic Calculus De Gruyter Textbook
ISBN: 9783110741254
3rd Edition
Authors: René L. Schilling, Björn Böttcher
Question Posted:





