Show that the vector (pi=left(pi_{1}=alpha, pi_{2}=beta, pi_{3}=gamma ight)), determined in example 8.6 , is a stationary initial

Question:

Show that the vector $\pi=\left(\pi_{1}=\alpha, \pi_{2}=\beta, \pi_{3}=\gamma\right)$, determined in example 8.6 , is a stationary initial distribution with regard to a Markov chain which has the one-step transition matrix (8.22) (page 349).

Data from 8.22

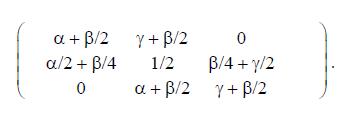
image text in transcribed

Data from Example 8.6

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Applied Probability And Stochastic Processes

ISBN: 9780367658496

2nd Edition

Authors: Frank Beichelt

See More Books

Question Posted: Apr 26, 2024 04:01 PM

See More Questions

Portray in words what transforms you would have to make to your execution to some degree (a) to accomplish this and remark on the benefits and detriments of this thought.You are approached to compose...
Consider the Markov Chain, Xn, on the states i = 0, 1, 2, . . . with transition matrix given by pi,i1 = p i = 1, 2, . . . pi,i+1 = 1 p i = 0, 1, . . . p0,0 = p where 0 < p < 1. (i) Show that the...
Python and most Python libraries are free to download or use, though many users use Python through a paid service. Paid services help IT organizations manage the risks associated with the use of...
Bollobs and Chung proposed a hybrid model that combines a 2-ring on $V$ vertices ( $V$ is even), plus a random matching. A matching is a graph in which every vertex has degree 1. To generate a...
A stock has a beta of 1.15, the expected return on the market is 10.3 percent, and the risk-free rate is 3.8 percent. What must the expected return on this stock be?
Job costing, consulting firm. Turner & Associates, a consulting firm, has the following condensed budget for 2011: Turner has a single direct-cost category (professional labor) and a single...
Derive Equation 8.45. C(t) = ko+ " E=1 kie-/ (8.45)
Accounting for Patents during 2007, Thompson Corporation spent $170,000 in research and development costs. As a result, a new product called the New Age Piano was patented. The patent was obtained on...
Charge q 1 = 7 nC is located at the coordinate system origin, while charge q 2 = 0 . 5 5 nC is located at ( a , 0 ) , where a = 0 . 7 5 m . The point P has coordinates ( a , b ) , where b = 0 . 2 5 m...
A source emits symbols 0 and 1 for transmission to a receiver. Random noises $S_{1}, S_{2}, \ldots$ successively and independently affect the transmission process of a symbol in the following way:...
Prove formulas (8.20), page 346 , for the mean times to absorption in a random walk with two absorbing barriers (example 8.3). Data from 8.20 Data from Example 8.3 1 1-(q/p)" m(n): p-q 1-(q/p). m(n)...
Liquid propane is burned with dry air. A volumetric analysis of the products of combustion yields the following volume percent composition on a dry basis: 8.6% CO2, 0.6% CO, 7.2% O2 and 83.6% N2....
1. Enter the Mexican Stock Exchange and choose a company of interest to you. 2. Download the performance of the company's shares, for a period of 20 to 30 days. 3. Generate a frequency distribution,...
The newspaper vending machine at the Food Lion near the corner of Charles Blvd. and Firetower Rd. historically has had a weekday demand of 30 papers 40% of the time, 31 papers 30% of the time, 32...
Your stockbroker suggests that you buy 1,000 shares of International Business Electronics (IBE). The stock currently is selling at $38.75 per share. From research over the internet you discovered...
After seeing a presentation on the power of data mining and hearing about your past consulting work, you are approached to create a model for a university's admissions office. The members of the...
A department's three-variance overhead standard costing system reported unfavorable spending and volume variances. The activity level selected for allocating overhead to the product was based on 80%...
A uniform plank of length 6.00 m and mass 30.0 kg rests horizontally across two horizontal bars of a scaffold. The bars are 4.50 m apart, and 1.50 m of the plank hangs over one side of the scaffold....
Show that every group G with identity e and such that x * x = e for all x G is abelian.
Writea 950-word paper in which you analyze Albert Bandura cognitive theories. Address the following items: Discuss the contributions that Albert Banduramade to the field of learning and cognition....
Simplify the following expressions: 1. (3+2) + (4-5) 3. (5-6) (3 - 2c) 5. (3-2)2 7. (2+3)2 9. (1+2)(6+ 3c) 2. (-7+9)+(2-10c) 4. (8+5)-(2 + 3c) 6. (4+)2 8. (2+4)(3 5) 10. (4-5)(2) 12. (3 + 4c)(3-4c)...
Discuss the emerging role of nuclear RNA metabolism in shaping gene expression programs and cellular phenotypes, including the regulation of alternative splicing, RNA editing, and non-coding RNA...

Show that the vector (pi=left(pi_{1}=alpha, pi_{2}=beta, pi_{3}=gamma ight)), determined in example 8.6 , is a stationary initial

Question:

+ /2 a/2 + /4 0 Y+B/2 0 1/2 B/4+y/2 + +/2 Y+B/2

Step by Step Answer:

Data ...View the full answer

Applied Probability And Stochastic Processes

Students also viewed these Business questions