The continuous random variable (X) is uniformly distributed on ([0,2]). (1) Draw the graph of the function
Question:
The continuous random variable \(X\) is uniformly distributed on \([0,2]\).
(1) Draw the graph of the function
\[p(\varepsilon)=P(|X-1| \geq \varepsilon)\]
in dependence of \(\varepsilon, 0 \leq \varepsilon \leq 1\).
(2) Compare this graph with the upper bound for the probability
\[P(|X-1| \geq \varepsilon)\]
given by the Chebyshev inequality, \(0 \leq \varepsilon \leq 1\).
(3) Try to improve the Chebyshev upper bound for
\[P(|X-1| \geq \varepsilon)\]
by the Markov upper bound (5.8) for \(a=3\) and \(a=4\).
Data from 5.8
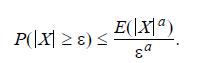
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Applied Probability And Stochastic Processes
ISBN: 9780367658496
2nd Edition
Authors: Frank Beichelt
Question Posted:





