The measurement error (X) of a measuring device has mean value (E(X)=0) and variance (operatorname{Var}(X)=0.16). The random
Question:
The measurement error \(X\) of a measuring device has mean value \(E(X)=0\) and variance \(\operatorname{Var}(X)=0.16\). The random outcomes of \(n\) independent measurements are \(X_{1}, X_{2}, \ldots, X_{n}\), i.e., the \(X_{i}\) are independent, identically as \(X\) distributed random variables.
(1) By the Chebyshev's inequality, determine the smallest integer \(n=n_{\text {min }}\) with property that the arithmetic mean of \(n\) measurements differs from \(E(X)=0\) by less than 0.1 with a probability of at least 0.99 .
(2) On the additional assumption that \(X\) is continuous with unimodal density and mode \(x_{m}=0\), solve (1) by applying the Gauss inequality (5.4).
(3) Solve (1) on condition that \(X=N(0,0.16)\).
Data from 5.4
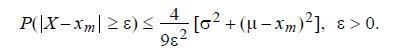
Step by Step Answer:

Applied Probability And Stochastic Processes
ISBN: 9780367658496
2nd Edition
Authors: Frank Beichelt





