This exercise concerns the Pareto distribution that proved to be a good model for many real variables such as the sizes of towns, files of Internet traffic, meteorites, sand particles, etc.

Consider a r.v. ξ₁ such that P(ξ₁ > x) = x^−α for x > 1 and a parameter α > 0. We call a Pareto distribution the distribution of any linear transformations of ξ₁; more precisely, the distribution of any r.v. ξ = bξ₁+d for arbitrary d and b > 0. The parameter b may be viewed as a scale parameter. Since ξ1 assumes values from [1, ∞) (say why!), the r.v. ξ takes on values from [b+d, ∞), so b+d may be called a location parameter.

Often, the term “Pareto distribution” is applied to the distribution with the tail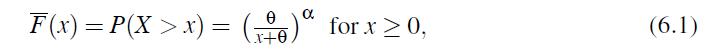

where the parameter θ > 0.

(a) Show that (6.1) corresponds to the distribution of the r.v. θ(ξ₁ −1).

(b) Find the mean and variance of the distribution (6.1). When do they exist?

Transcribed Image Text:

F(x) = P(X > x) = (4) for x 0, (6.1)