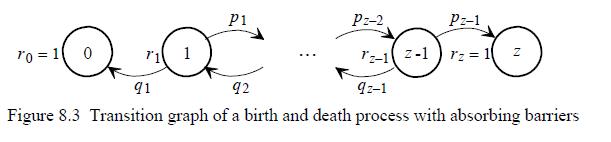
Two gamblers 1 and 2 begin a game with stakes of sizes \(\$ 3\) and \(\$ 4\), respectively. After each move a gambler either wins or loses \(\$ 1\) or the gambler's stake remains constant. These possibilities are controlled by the transition probabilities

\[\begin{aligned} & p_{0}=0, p_{1}=0.5, p_{2}=0.4, p_{3}=0.2, p_{4}=0.4, p_{5}=0.5, p_{6}=0.6, p_{7}=0 \\ & q_{7}=0, q_{6}=0.5, q_{5}=0.4, q_{4}=0.2, q_{3}=0.4, q_{2}=0.5, q_{1}=0.6, q_{0}=0 \end{aligned}\]

(According to Figure 8.3 there is \(p_{i}=p_{i i+1}\) and \(q_{i}=p_{i i-1}\).) The game is finished as soon as a gambler has won the entire stake of the other one or, equivalently, if one gambler has lost her/his entire stake.

(1) Determine the probability that gambler 1 wins.

(2) Determine the mean time till any of the gamblers win.

Data from Figure 8.3

P1 Pz-2 Pz-1 10=10 71 1 12-12-12 = 12 91 92 92-1 Figure 8.3 Transition graph of a birth and death process with absorbing barriers