Question: Suppose a Markov chain with unique positive stationary distribution Ï starts at state i. The expected number of steps until the chain revisits i is

Suppose a Markov chain with unique positive stationary distribution Ï€ starts at state i. The expected number of steps until the chain revisits i is called the expected return time of state i.We state without proof that the expected return time of state i is equal to 1/Ï€_i. Find the expected return time of the center vertex in the lollipop graph of Figure 10.14.

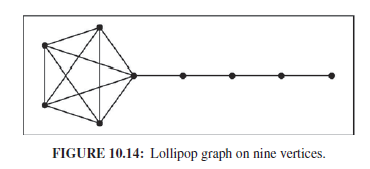
FIGURE 10.14: Lollipop graph on nine vertices.

Step by Step Solution

★★★★★

3.33 Rating (156 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

The stationary proba... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Probability With Applications Questions!

For a Markov chain with each of the transition probability matrices in (a)( c), find the communicating classes and the periodicity of the various states. (a) (b) (c) 0 1001-3 0 0 1-2 1-3 011-2 1-3...

Write down the Metropolis-Hastings algorithm for simulating a Markov chain with stationary distribution = (1/6, 2/3, 1/6), using the proposal transition matrix 0 /2 0 1/2 0 1/2 1/2/

In tossing three fair coins, let the random variable X be defined as X = number of tails. Then the distribution of X is given by Write down the Metropolis or Metropolis-Hastings algorithm for...

A rat runs through the maze shown below. At each step it leaves or stay by choosing at random one of the doors with equal probability. For example, if it is in room 0, it can has two options: stay at...

Chapter 5 Discrete Markov process Suppose we have a sequence of random variables, {X0 , X1 , . . .} = {Xn } , which is also n=0 called a stochastic process. In this chapter, we study a commonly used...

EE 351K Probability, Statistics and Stochastic Processes - Spring 2016 Homework 12 Topics: Random Processes, Markov Chain Homework and Exam Grading \"Philosophy\" Answering a question is not just...

nodes, but at least its bias can be quantified by Markov Chain L. INTRODUCTION analysis and thus can be corrected via appropriate re-weighting The popularity of online social networks (OSNs) in...

Answer all please give eexplanations The mean number of customers appearing in a bank during a self-assertively picked hour is four. The bank boss is contemplating reducing the amount of tellers....

Answer appropriately Consider a Markov chain {Xn, n = 0, 1, . ..} on the state space S = {0, 1, 2}. Suppose that the Markov chain has the transition matrix 2 10 10 10 2 P = 3 10 2 4 10 10 1. Show...

THe answers should be detailed. THank you. A rat runs through the maze shown below. At each step it leaves the room it is in by choosing at random one of the doors out of the room. 2 3 4 5 6 (a) Give...

You are thinking about buying a stock and holding it for 2 years. You expect that the stock will pay a dividend of $0.79 in 1 year and $2.19 in two years. You expect to sell for $100.35 in 2 years....

How should a company select an outsourcing provider?

5. Sole Proprietorships What are the disadvantages of the sole proprietorship form of business?

=+3. Why should you develop a budget?

Now perform the test using the exact method and obtain a 2-sided p-value? Cardiovascular Disease Left ventricular mass (LVM) is an important risk factor for subsequent cardiovascular disease. A study...

Compare your results in Problems 9.69 and 9.70? Cardiovascular Disease Left ventricular mass (LVM) is an important risk factor for subsequent cardiovascular disease. A study is proposed to assess the...

Compare your results to those obtained using t test methods in Problem 8.107 (p. 329)? Cardiovascular Disease Left ventricular mass (LVM) is an important risk factor for subsequent cardiovascular...

You are a publicly listed Australian company who manufactures tens of thousands of plastic toys. Your toys meet foreign standards for toy products and are legally sold in foreign markets. The toys...

are as shown: What is the allocation of the budget among the three media? What is the total audience reached? Increase in audience coverage of approximately

The COVID-19 pandemic had changed the working lifestyle of many people. Work-from-home policy had caused most workers to be more sedentary. We sit hours and hours in front of our computers and often...