Question: The joint probability mass function of X and Y is x = 0, 1, ... , y = 0, 1, ... ,x. (a) Find the

The joint probability mass function of X and Y is

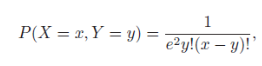
P(X = x,Y = y) = e²y!(x – y)! |

x = 0, 1, ... , y = 0, 1, ... ,x.

(a) Find the conditional distribution of Y given X = x.
(b) Describe the distribution in terms of distributions that you know.
(c) Without doing any calculations, find E[Y|X = x] and V[Y|X = x].

P(X = x,Y = y) = ey!(x y)! |

Step by Step Solution

★★★★★

3.36 Rating (159 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a The marginal distribution of X is for x 0 1 ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Probability With Applications Questions!

In a piston assembly, the specifications for the clearance between piston rings and the cylinder wall are very tight. In a lot of assemblies, let X be the number with too little clearance and let Y...

Refer to Exercise 1. a. Find the conditional probability mass function p Y |X (y |0). b. Find the conditional probability mass function p X|Y (x |1). c. Find the conditional expectation E(Y | X = 0)....

Automobile engines and transmissions are produced on assembly lines, and are inspected for defects after they come off their assembly lines. Those with defects are repaired. Let X represent the...

The joint probability mass function of X and Y is given by ,(1, 1) = 0.20, ,(1, 2) = 0.4, ,(2, 1) =0.25, ,(2, 2) = 0.15Find the each of the following. Give exact answers using fraction or decimal. a....

1. There are 16 pea seeds in a packet available to a gardener. Seven of the peas areWando, 4 are Maestro, and 5 are Lincoln. To test the soil of a specific garden for growing peas, the gardener picks...

Dorcas has an advantageous TV. The TV uses two batteries and both of them are dead. Influence opens another pack of four incredible batteries and dumps them on the table. By then he opens the TV and...

41. The joint probability mass function of X and Y is given by $$ p(1, 1) = \frac{1}{8} $$ $$ p(1, 2) = \frac{1}{4} $$ $$ p(2, 1) = \frac{1}{8} $$ $$ p(2, 2) = \frac{1}{4} $$ (a) Compute the...

4-12. Let a random variable X be defined as the number of heads obtained in two flips of a fair coin. Determine the sample space S and the associated (discrete) probability distribution. Verify that...

Given below is the joint probability mass function of X and Y: 1 0 0 0.2 0.1 Y 1 0.1 0.0 0.2 2 0.2 0.2 (a) Find E(Y)X=2) and E [Y?1X = 2] (b) VAR(YX=2) 2.

Solve for the maximum of the following equation for 0<=b<=1, where Q is a positive semidefinite 3*3 symmetric matrix, a is in R^3. 2Qx+ Q tA ~b+?y 27

An iron bar of length 1.4 m has a diameter of 2 cm and a uniform magnetization of 1.72 ? 10 6 A/m directed along the bar's length. The bar is stationary in space and is suddenly demagnetized so that...

Eli Lilly bonds have an annual coupon rate of 5.55% and a par value of $1,000 and will mature in 17 years. If you require a 5 percent return, what price would you be willing to pay for a Eli Lilly...

2.3. Customers arrive at a checkout station in a market according to a Poisson process of rate A = 1 customer per minute. The checkout station can be operated with or without a bagger. The checkout...

In the federal governments Current Population Survey, the response rate for 20- to 29 year olds is 85%; for individuals at least 70 years of age it is 99%. Why do you think this is?

During every election, pollsters conduct exit polls to help determine which candidate people voted for. During the 2004 presidential election, pollsters incorrectly predicted John Kerry the winner...

Name two biases that led to the Literary Digest making an incorrect prediction in the presidential election of 1936?

I need help on question C and D The following frequency histogram presents the final grades of a random sample of 100 college studen 183 15 - 12 - Frequency LO 63 66 69 72 90 93 96 Final Grade Score...

The mean clotting time of blood is 7.45 seconds with a standard deviation of 3.6 seconds. What is the probability that an individual's clotting time will be less than 3 seconds or greater than 8...

15. A share of common stock has just paid a dividend of $2.00. If the expected long-run growth rate for this stock is 15 percent, and if investors require a 19 percent rate of return, what is the...