Consider the action for a (Dirac) spinor,

written in terms of independent variables \(\psi\) and \(\psi^{*}\). Calculate the primary constraints and the total Hamiltonian \(H_{T}\). Check that there are no secondary constraints, and then from

solve for \(U_{m}, v_{A}\). Note that classical fermions are anticommuting, so we defined \(p\) by taking the derivatives from the left, for example \(\frac{\partial}{\partial \psi}(\psi \chi)=\chi\), so that \(\left\{p^{A}, q_{B}\right\}=-\delta_{B}^{A}\). In general, we must define

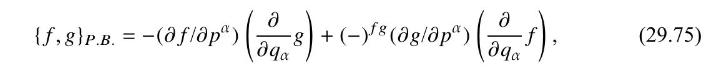
where \(\partial f / \partial p^{\alpha}\) is the right derivative, for example \(\frac{\partial}{\partial \psi}(\chi \psi)=\chi\), and \((-)^{f g}=-1\) if \(f\) and \(g\) are both fermions and +1 otherwise (if \(f\) and/or \(g\) is bosonic). This bracket is antisymmetric if \(f\) and \(g\) are bose-bose or bose-fermi, and symmetric if \(f\) and \(g\) are both fermionic.

Transcribed Image Text:

S s = at(i*), (29.73)