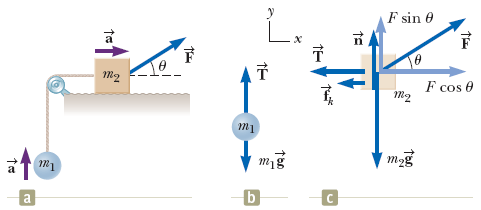
A block of mass m ₂ on a rough, horizontal surface is connected to a ball of mass m ₁ by a lightweight cord over a lightweight, frictionless pulley as shown in figure (a). A force of magnitude F at an angle ? with the horizontal is applied to the block as shown and the block slides to the right. The coefficient of kinetic friction between the block and surface is ? _k . Determine the magnitude of the acceleration of the two objects.

Conceptualize Imagine what happens as F(vector) is applied to the block. Assuming F(vector) is not large enough to lift the block, the block slides to the right and the ball rises.

Categorize We can identify forces and we want an acceleration, so we categorize this problem as one involving two particles under a net force, the ball and the block. Analyze First draw free-body diagrams for the two objects as shown in figures (b) and (c). The applied force F(vector) has x and y components F cos( ? ) and F sin( ? ), respectively. Because the two objects are connected, we can equate the magnitudes of the x component of the acceleration of the block and the y component of the acceleration of the ball and call them both a . Let us assume the motion of the block is to the right.

Apply the particle under a net force model to the block in the horizontal direction:

(1) ? F _x = F cos( ? ) - f _k - T = m ₂ a _x = m ₂ a

Apply the particle in equilibrium model to the block in the vertical direction:

(2) ? F _y = n + F sin( ? ) - m ₂ g = 0

Apply the particle under a net force model to the ball in the vertical direction:

(3) ? F _y = T - m ₁ g = m ₁ a _y = m ₁ a

Solve Equation (2) for n :

n = m ₂ g - F sin( ? )

Substitute n into f _k = ? _k n from the above equation:

(4) f _k = ? _k ( m ₂ g - F sin( ? ))

Substitute Equation (4) and the value of T from Equation (3) into Equation (1):

F cos( ? ) - ? _k ( m ₂ g - F sin( ? )) - m ₁ ( a + g ) = m ₂ a

Solve for a in terms of ? _k , m ₁ , m ₂ , g , and a = ?

Finalize The acceleration of the block can be either to the right or to the left depending on the sign of the numerator in Equation (5). If the motion is to the left, we must reverse the sign of f _k in Equation (1) because the force of kinetic friction must oppose the motion of the block relative to the surface. In this case, the value of a is the same as in Equation (5), with the two plus signs in the numerator changed to minus signs.

Consider the system described in the example with m ₁ = 0.51 kg and m ₂ = 0.40 kg. The coefficient of static friction between the block and the surface is 0.45. The angle ? of the force F is equal to 20.0?. If F = 0, you can easily show that the block will accelerate to the left since the maximum static friction force is not sufficient to keep the block at rest. If F is sufficiently large, it is clear that the block will accelerate to the right. Find the range of F that allows the system to remain at rest. F _min = N F _max = N

Transcribed Image Text:

a m1 the N m2 F Ť L. ↑E my b mig T tuk C 18 F sin 0 mq m₂g F cos 0 a m1 the N m2 F Ť L. ↑E my b mig T tuk C 18 F sin 0 mq m₂g F cos 0

Answer rating: 100% (QA)

Draw the freebody diagram of the mass m 1 Apply Newtons second law to mass m 1 which is moving with acceleration a in upward direction Here T is the tension force in the cable and g is the acceleratio... View the full answer