According to the result stated in Problem 1 and 2, the characteristic polynomial of 3 x 3 matrix A is given by The remaining coefficient c1 can be found by substituting ? = 1 and then calculating the two determinants

According to the result stated in Problem 1 and 2, the characteristic polynomial

of 3 x 3 matrix A is given by

The remaining coefficient c1 can be found by substituting ? = 1 and then calculating the two determinants |A| and p(1) = |A - 1|. Use this method to find the characteristic equation, eigenvalues, and associated eigenvectors of the matrix.

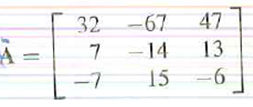
Problem 1:

Suppose that the characteristic equation IA - AAI = 0 is written as a polynomial equation (Eq. (5)). Show that the constant term is co = det A. Suggestion: Substitute an appropriate value for A.

Problem 2:

If A = [aij] is an n x n matrix, then the trace Tr A of A is defined to be

The sum of the diagonal elements of A. It can be proved that the coefficient of ?n - 1 in Eq. (5) is cn -1 = (-1) n - 1 (Tr A). Show explicitly that this is true in the case of a 2 x 2 matrix.

Transcribed Image Text:

P(X) = |A-XII p(x)=x² + (TrA)^²+₁2+ (det A). A = 32 -67 7-14 47 13 -7 15-6 TrA= a₁ +922 +· + Anns

• Expert Answer

First find the trace and determinant of the matrix given Expand the determina View the full answer